Robotics - Chapter 3. Manipulator Kinematics
Manipulator는 링크(Link)와 이들을 연결하는 관절(Joint)의 조합으로 구성되어있으며, 관절은 인접한 두 링크를 연결하고 상대적인 운동을 가능하게 한다. 관절의 움직임에 의해서 공간상에서 Manipulator의 자세뿐만 아니라, End-effector의 position과 orientation이 결정된다.
Manipulator의 관절을 움직여서 End-effector가 특정한 위치에 도달해서 작업 대상물을 잡거나 집어 올리거나, 다른 위치로 이동시키는 등의 일련의 과정을 운동 또는 모션(Motion)이라고 한다. Manipulator가 어떤 목적에 부합하게 움직이도록 하는 것을 모션 제어(Motion control)이라고 한다. 다시 말하면, 로봇의 링크와 링크를 연결하는 관절을 유효한 범위에서 적절하게 제어하는 것이 모션 제어이며, Kinematics는 이러한 모션 제어에 기초가 되는 학문이다.
3차원상에서 기구물의 Pose를 결정하기 위해 기구물의 position 및 orientation을 정의하는 것이 Kinematics(기구학)이다. 따라서, Kinematics에서는 기구물의 위치(position)와 방위(orientation)를 결정하는 요소인 링크의 길이와 관절의 각도 및 속도/가속도 등에 대한 정보는 이용하지만, 기구물의 운동을 유발할 수 있거나 운동을 지속할 수 있도록 하는 힘에 대한 사항은 고려하지 않는다.
힘에 대한 사항을 고려하는 것은 Kinetics에서 배운다.
관절과 자유도
Manipulator는 연쇄적인 링크와 링크를 관절로 연결한 기구물의 조합이라고 할 수 있다. Manipulator의 동작이 관절을 중심으로 일어나기 때문에 관절을 축(Axis)이라고 표현하기도 한다. 관절은 이웃한 한 쌍의 링크를 연결하기 때문에 관절의 움직임에 따라 링크가 연결된 모습 즉, Manipulator의 자세가 결정된다.
일반적인 산업용 로봇이나 Manipulator에 적용되는 관절의 유형은 회전(Revolute) 관절이나 직동(Prismatic) 관절 또는 미끄럼 관절로 구성된다. 여러 관절로 구성되는 Manipulator의 경우 회전 관절을 $R$, 직동 관절은 $P$로 나타내며, 구성의 순서에 따라 Base부터 End-effector 순서로 각 관절을 표시한다. 예를 들어 회전 Base 관절과 회전 손목 관절을 가지고 있는 Manipulator는 $RR$형, 회전 Base 관절과 직동 손목 관절을 가지고 있는 Manipulator는 $RP$형 등으로 구분할 수 있다.
Manipulator의 각 관절은 1개의 자유도(Degrees of Freedom, dof)를 갖는 것이 일반적이며, Kinematics 또는 Manipulator에서의 자유도란 Manipulator의 Pose를 결정하기 위해 필요한 최소한의 좌표계 변수 개수를 의미한다. 또는 기구물의 Pose나 상태를 설명하는데 필요한 독립변수의 개수라고 할 수 있다.
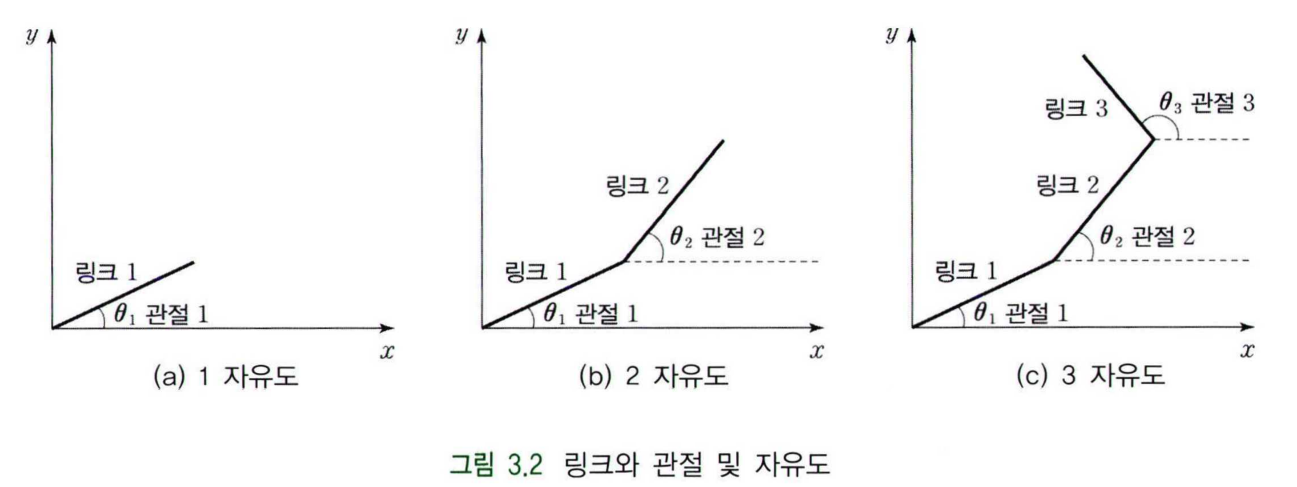
자유도에 관한 예시를 살펴보자. (a)에서는 하나의 링크와 원점의 회전 관절 하나로 이루어져있으며, 회전 관절 값 하나( $\theta_1$ )만으로 로봇의 말단의 position 및 orientation을 나타낼 수 있기 때문에 1 자유도 Manipulator라고 할 수 있다. (b)의 경우에는 링크가 2개 있으며, 두 링크는 관절 2에 의해 연결되어 있다. 링크 1의 말단은 관절 1( $\theta_1$ )에 의해서 온전히 position 및 orientation이 결정될 수 있으나, 링크2의 말단의 position 및 orientation은 관절 1( $\theta_1$ )과 관절 2( $\theta_2$ ) 모두에 dependent하다. 따라서, 이러한 경우 Manipulator는 2개의 독립된 관절에 의해서 position 및 orientation이 결정되므로 2 자유도를 갖는다. 같은 방법으로 (c)의 경우는 3 자유도임을 알 수 있다.
위 예시의 Manipulator의 움직임 형태를 유심히 살펴보면 $z$축 방향으로의 비틀림이나 회전이 없이 $xy$평면 상에서만 동작하는 것을 볼 수 있다. 이러한 평면상의 기구에 대한 자유도는 Manipulator의 Base부를 링크로 포함시키는 Kutzbach의 공식을 이용해서 쉽게 파악할 수 있다.
\[\text{DoF} = 3(L-1)-2J_1-J_2\]위 식에서 $L$은 링크의 개수, $J_k$는 자유도가 $k$인 관절의 개수를 나타낸다. 앞서 설명했듯이 Base부를 링크로 포함시키기 때문에 (a)에서는 링크의 수가 총 2개, (b)에서는 3개, (c)에서는 4개가 된다. 평면 상의 움직임뿐만 아니라, 공간 상의 움직임을 가지는 Manipulator의 자유도까지 구할 수 있는 일반적인 공식은 다음과 같다.
\[\text{DoF} = \lambda(L-A-1)-\sum^n_{i=1}f_i\]이때 $\lambda$는 움직임이 공간 상일 경우에는 6, 평면 상일 경우에는 3이 된다. $L$은 링크의 개수, $A$는 관절의 개수, $f_i$는 $i$번째 관절의 자유도를 의미한다. $A$와 $f_i$를 적절하게 조작하면 이전 식의 $J_i$와 같은 꼴로 바꿀 수 있다.
관절과 링크의 표현
무거운 물체를 들어 올리거나 이동시키는 등의 작업을 성공적으로 수행하기 위해서는 링크의 중량, 강도, 강성, 관성저항 등의 요소들을 면밀하게 검토해야 한다. 하지만, Manipulator의 Kinematics에서는 이러한 설계 요소를 고려하지 않고, 링크는 외력에 의해 모양이나 크기가 변형되지 않는 완전한 강체(Rigid body)로 가정한다.
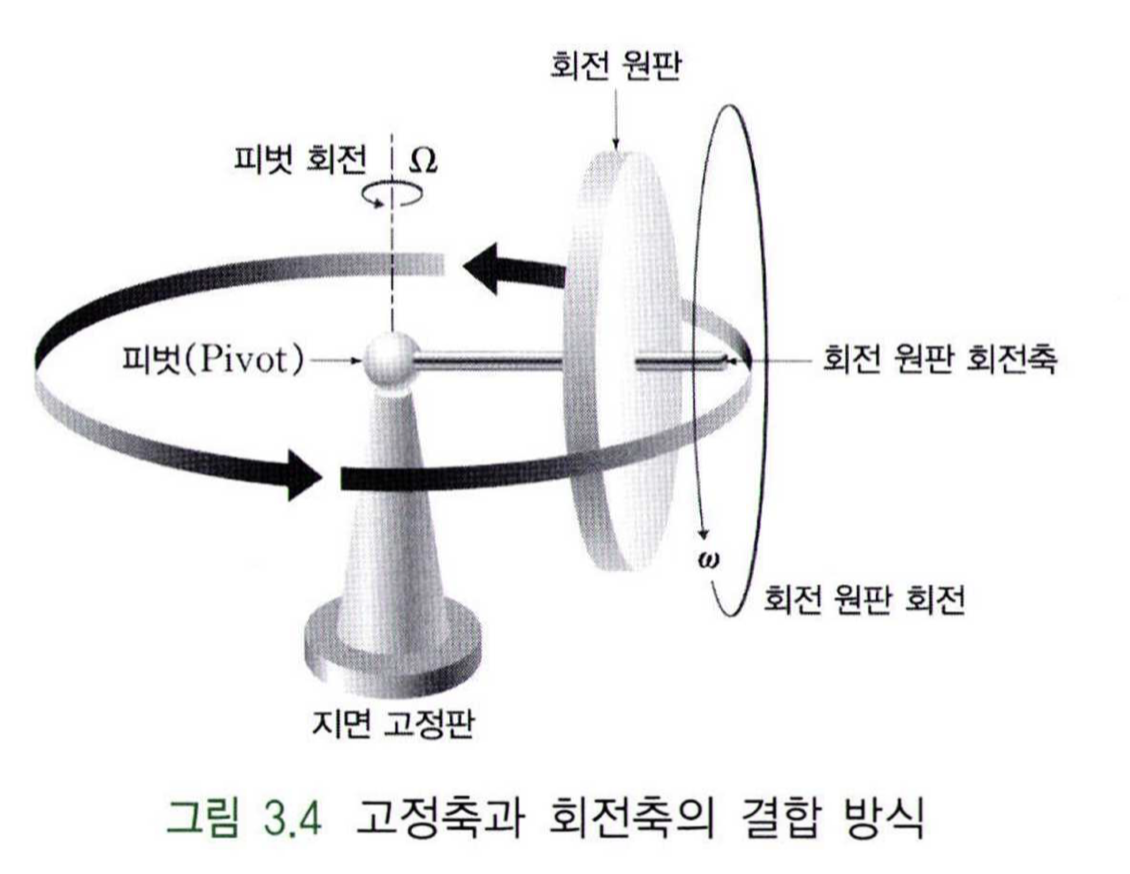
회전 관절은 고정된 회전축을 중심으로 회전이 이루어지는 고정축 또는 단순 링크가 기구적으로 연결되어야만 회전할 수 있게 된다. 고정축에 대한 이해를 돕기 위해 아래와 같은 회전 원판(자이로, Gyro)의 구성을 살펴보자.
피벗(Pivot) 부분은 지면에 고정축을 중심으로 회전되는 회전부와 회전 원판을 연결시켜주는 고정 링크로 구성되어 있다. 다시 말해, 피벗은 지면 고정판의 축을 중심으로 회전하고 이 피벗에 피벗 링크가 수평 방향으로 연결되어 있다. 피벗 링크는 피벗에 고정된 고정 링크이므로, 말단부에 연결된 회전 원판은 자체적으로 회전이 일어남을 알 수 있다.
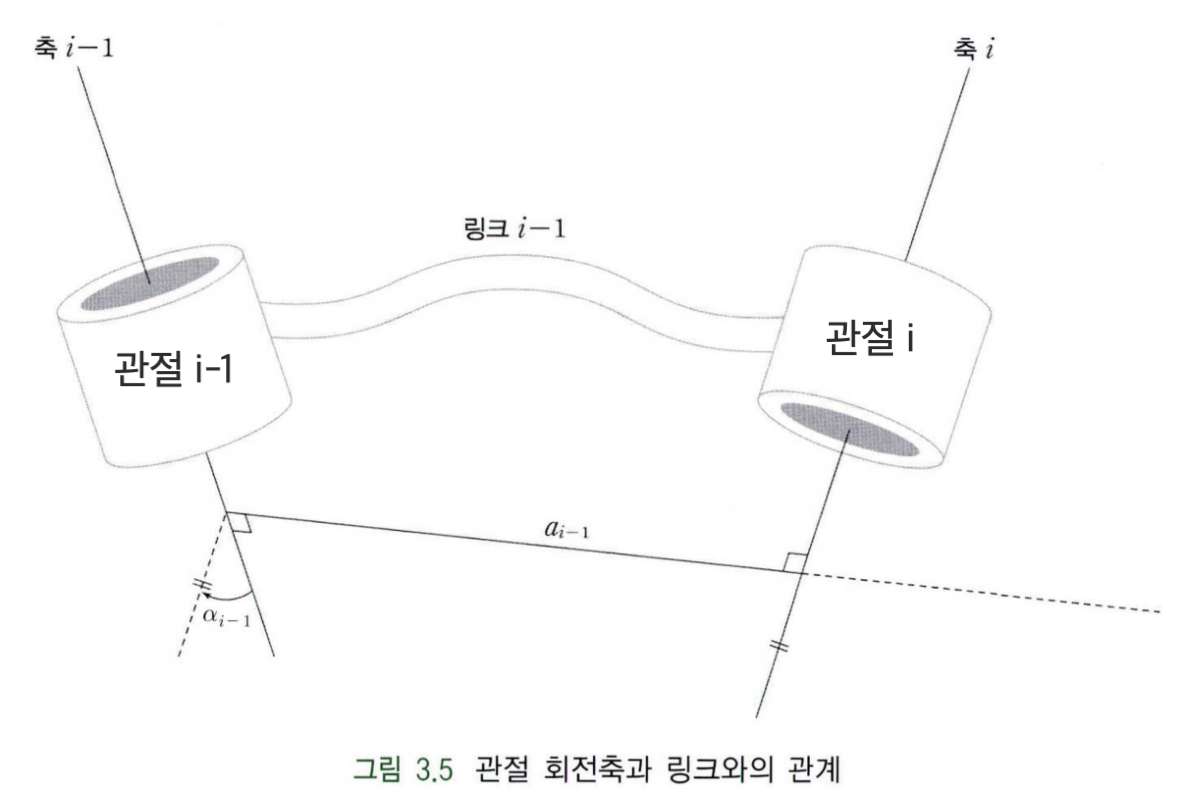
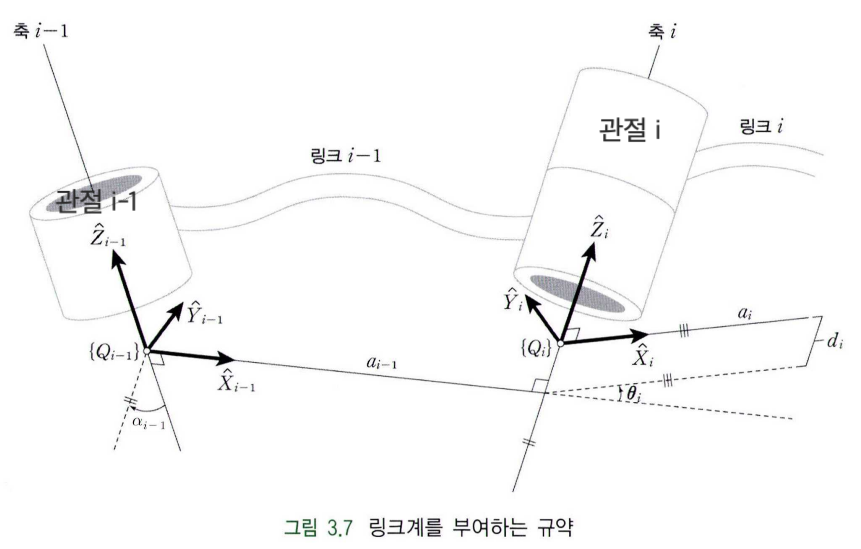
위 그림에서는 관절 $i-1$과 관절 $i$를 연결하는 링크가 길이($a_{i-1}$)와 비틀림($\alpha_{i-1}$)의 두 인자로 표현되어 있다. 링크에 연결된 관절축의 중심은 실선으로 나타내며, 관절축의 방향은 관절 $i-1$과 관절 $i$가 서로 이웃할 경우 관절 $i-1$에서 관절 $i$로의 벡터로 지정한다. (관절은 원기둥 모양으로 표현되어있고, 링크는 띠 형태로 표현되어 있다.)
기구학적으로 관절이 회전되려면 고정축이 필요한데, 관절 $i-1$에서 나와서 다음 관절을 연결하는 링크 $i-1$의 끝부분이 관절 $i$를 위한 고정축이라 정의할 수 있다. 다시 말해, 관절 $i-1$은 링크 $i-2$의 끝 부분의 고정축 위에 놓인 회전 관절이고, 관절 $i$는 링크 $i-1$의 끝 부분의 고정축 위에 놓인 회전 관절이다. 기하학적으로 두 직선 간의 최단 거리는 두 직선에 서로 수직인 유일한 직선으로 정의되기 때문에, 서로 다른 두 관절 $i-1$과 $i$를 연결하는 최단거리 $\boldsymbol{a_{i-1}}$은 $i-1$번째 링크의 길이(Link length)가 된다.
관절 $i-1$의 회전축에 $a_{i-1}$이 수직으로 만나는 부분($\alpha_{i-1}$이 표현된 부분)에서 관절 $i$와 평행한 선분을 점선으로 표현되어 있는데, 이는 관절 $i$의 회전축을 관절 $i-1$의 회전축에 투영시킨 것으로 생각할 수 있으며, 이때 두 선분이 이루는 각의 값이 $\boldsymbol{\alpha_{i-1}}$이고 이를 링크 $i-1$의 비틀림 각(Link twist angle)이라고 정의한다.
이때 비틀림각 $\alpha_{i-1}$은 축 $i-1$에서 축 $i$ 방향이 양의 방향으로 정의되어 있음에 유의하자.
위에서 표현된 링크의 길이($a_{i-1}$)와 비틀림 각($\alpha_{i-1}$)은 모두 이후에 나오는 [D-H 표기법]에 의해 정의된 값이다.
관절 변수
Manipulator의 링크 설계 시에 고려되어야 하는 사항들이 있었들이, 서로 다른 두 링크를 연결하는 관절의 설계 과정에서도 관절의 강도, 회전에 필요한 베어링, 기어 등과 같은 요소를 반영해야만 한다. 하지만, 기구학적인 측면에서는 연결된 두 링크에 대한 관계만을 고려해서 단순화할 수 있다.
관절의 강도: 관절이 견딜 수 있는 최대 하중이나 스트레스를 의미한다. 이는 관절이 파손되지 않고 안정적으로 작동할 수 있는 한계를 나타낸다.
베어링: 로봇이나 기계의 회전 부분이 부드럽고 정확하게 움직일 수 있도록 한다. 또한, 부품 사이의 마찰을 감소시켜 에너지 소비를 줄이고, 수명을 연장하는 데 중요한 역할을 한다.
기어: 기계적 에너지를 전달하고, 회전 속도나 토크를 변환하기 위해 사용되는, 둘레에 치아가 있는 휠 또는 디스크이다.
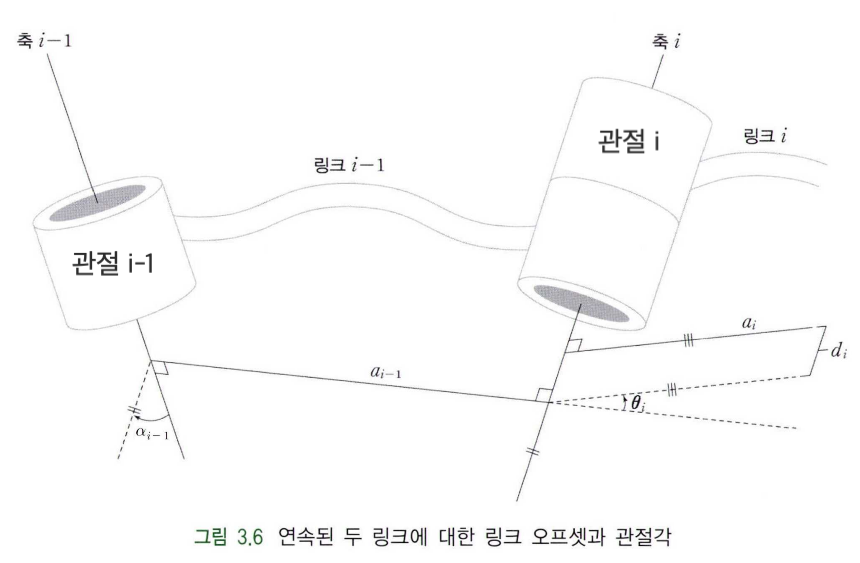
두 개의 연속된 링크의 상대 위치와 회전을 나타내기 위해서는 위와 같이 하나의 회전 관절($i-1$)에서 나온 링크의 끝에 고정된 축 상에 다른 회전 관절($i$)이 놓여야 한다. 즉, 서로 다른 링크의 연결 부위에 하나의 회전축을 공통으로 포함해야만 한다. 또한 $a_{i-1}$을 구할 때와 마찬가지로, 관절 $i$와 관절 $i+1$ 사이의 최단 거리를 $a_i$(링크 $i$의 길이)라고 표현할 수 있다.
이전과는 다르게 축 $i$에 두개의 원기둥이 놓여있다. 하단의 원기둥은 링크 $i-1$의 끝부분을 나타내고, 상단의 원기둥은 회전 관절 $i$를 나타낸다.
링크 $i-1$과 링크 $i$를 연결하는 공통의 회전축 $i$는 각 링크의 길이를 나타내는 법선 $a_{i-1}$과 $a_i$와 만나는 두 점을 정의할 수 있다. 이때 회전축 $i$ 상에서 두 점 사이의 거리를 $d_i$라 하면, 이는 링크 $i-1$과 링크 $i$가 떨어진 거리를 나타내며 링크 오프셋(Link offset)이라고 한다. 관절 $i$가 직동 관절일 경우 $d_i$는 관절이 늘어난 정도에 따라 값이 변하는 변수가 된다.
그리고 축 $i$의 두 법선 $a_{i-1}$과 $a_i$가 이루는 각의 크기를 $\theta_i$라 하면, 이를 관절 각도(Joint angle)라고 정의한다. 관절 $i$가 회전 관절일 경우 $\theta_i$는 관절이 회전한 정도에 따라 값이 변하는 변수가 된다.
| 기호 | 이름 | 설명 |
|---|---|---|
| $a_{i-1}$ | 링크 길이 | 축 $i$와 축 $i-1$ 사이의 거리 |
| $\alpha_{i-1}$ | 링크 비틀림 각도 | 축 $i$가 축 $i-1$에 비해 비틀린 정도 |
| $d_i$ | 링크 오프셋 | 축 $i$의 두 법선 $a_{i-1}$과 $a_i$ 사이의 거리 |
| $\theta_{i}$ | 관절 각도 | 축 $i$의 두 법선 $a_{i-1}$과 $a_i$가 이루는 각 |
설명은 모두 $i-1$과 $i$ 사이의 관계이지만, 기호의 subscript는 조금씩 다름에 주의하자.
Manipulator의 좌표계 설정
앞서 설명한 그림처럼 각 링크가 이전 링크에 대해 단 하나의 자유도를 가지는 경우, Manipulator의 Base 관절에서부터 순서대로 연결된 모든 관절에 대해서 좌표계를 부여하고 이들의 관계를 동차 변환을 이용하여 상대적으로 표현할 수 있다. 이때 각 링크는 4개의 값($a_i, \alpha_i, d_i, \theta_i$)으로 표현된다. 회전 관절인 경우에는 관절 각도에 따라서 pose를 확정할 수 있기 때문에 $\boldsymbol{\theta_i}$가 관절 변수가 되고, 나머지 3개의 요소는 고정된 링크 인자가 된다. 직동 관절인 경우에는 하나의 관절이 축을 따라 이동하는 거리에 따라 pose를 결정할 수 있기 때문에 관절 간격인 $\boldsymbol{d_i}$가 관절 변수가 되고, 나머지 3개의 요소가 고정된 링크 인자가 된다.
Manipulator에 좌표계를 설정하는 방법은 D-H 표기법(Denavit-Hartenberg convention, DH method)이 사용된다.
정확히 말하자면 Modified DH method가 사용된다. Standard DH method와는 x, y, z 축이나 관절/링크의 index를 설정하는 방식이 조금씩 다르다.
1. Manipulator의 연결된 링크에 대한 좌표계 설정
Manipulator의 링크들의 상대적인 위치를 기술하기 위하여, 각 링크의 번호와 같은 번호를 갖는 좌표계를 부여한다. 즉, 링크계 {$Q_i$}는 링크 $i$에 부여된 링크 좌표계이다.
위와 같이 링크에 부여된 링크계의 $\hat Z$축은 해당 관절축의 벡터 방향과 일치시킨다. 즉, 링크계 {$Q_i$}의 $\hat Z_i$축은 관절축 $i$의 벡터와 동일하다. 또한 원점은 관절축 $i$와 법선 $a_i$가 만나는 지점으로 설정하고, $\hat X_i$축은 법선 $a_i$ 상에서 다음 관절축 $i+1$을 향하는 방향으로 설정한다. 마지막으로 $\hat Y_i$축은 이미 설정한 $\hat Z_i$축과 $\hat X_i$축을 기준으로 오른손 법칙에 따라 결정한다.
2. Manipulator의 Base와 End-effector에 대한 좌표계 설정
Manipulator는 지면에 고정될 수 있도록 고정면을 바닥에 고정한 후, 그 위에 회전 관절을 두어 Base를 만드는 경우가 대부분이다. 이때, 지면에 고정되는 부분을 링크계 {0}으로 지정하는데, 이는 Manipulator의 기구학적인 문제를 해석하는데 필요한 기준 좌표계로서의 역할을 한다.
Base 좌표계 {0}은 첫번째 관절 변수($d_1~ \text{or}~ \theta_1$)가 0일 때의 좌표계 {1}의 방향과 동일하게 좌표계를 설정해준다. 원점은 기반면 혹은 좌표계 {1}과 동일하게 설정하는 것이 일반적이다.
마지막 링크는 다음 링크가 존재 하지 않아서 기존의 방법으로는 $\hat X$축과 원점을 설정할 수 없다. 그래서 마지막 링크계의 $\hat X$축과 원점을 설정하는 방법을 정해주어야 한다. 회전 관절과 직동 관절 모두 $\hat X_n$의 방향을 $\theta_n=0$일 때, $\hat X_{n-1}$과 같은 선상으로 정렬하고, 링크계의 원점은 $d_n=0$인 지점에 설정한다. 즉, 두 경우 모두 회전축 $\hat Z_n$의 방향이 $\hat Z_{n-1}$과 동일하다면 $\theta_n=d_n=0$ 일 때, 링크계 {n}은 링크계 {n-1}과 같은 방향의 좌표계를 가진다. 단, 일반적으로 $a_{i-1}\neq 0$ 이기 때문에 원점은 동일하지 않다.
그리고 마지막 링크의 말단부(End-effector)의 좌표계 {n+1}은 좌표계 {n}과 동일한 방향을 가지도록 설정해준다. 이때도 마찬가지로 일반적으로는 $a_{i}\neq 0$ 이기 때문에 원점은 동일하지 않다.
3. 링크계 설정을 위한 링크인자 정의 및 좌표계 설정 순서
| 기호 | 이름 | 설명 | 기준 축 | 변수 가능 여부 |
|---|---|---|---|---|
| $a_{i-1}$ | 링크 길이 | $\hat Z_{i-1}\sim\hat Z_{i}$축 사이의 최단 거리 | $\hat X_{i-1}$ | X |
| $\alpha_{i-1}$ | 링크 비틀림 각도 | $\hat Z_{i-1}\sim\hat Z_{i}$축 사이의 비틀림 각 | $\hat X_{i-1}$ | X |
| $d_i$ | 링크 오프셋 | $\hat X_{i-1}\sim\hat X_{i}$축 사이의 최단 거리 | $\hat Z_{i}$ | O |
| $\theta_{i}$ | 관절 각도 | $\hat Z_i$축 중심으로 회전한 각 | $\hat Z_{i}$ | O |
각도($\alpha_{i-1},\theta_{i}$)는 기준 축을 중심으로 시계 방향의 회전이 양의 방향이다. 거리($a_{i-1},d_i$)는 기준 축의 방향과 부호가 동일하다.
각 링크 간의 관계는 앞서 정의한 위 4개의 링크 인자($\boldsymbol{a_i}, \boldsymbol{\alpha_i}, \boldsymbol{d_i}, \boldsymbol{\theta_i}$)를 사용해 표현할 수 있다.
링크계를 부여하는 순서와 영점(Zero position)을 정하는 방법은 다음과 같다.
- 링크 번호를 고정된 Manipulator의 바닥면 $0$에서부터 마지막 링크 $n$까지 순서대로 할당한다.
- 링크와 링크를 연결하는 모든 관절에 대해서 관절의 기준 축(회전 관절은 회전축, 직동 관절을 운동 방향)을 $\hat Z$축으로 지정하고, 각 축을 관통하는 연장선을 그린다.
- 서로 이웃하는 $\hat Z_i$축과 $\hat Z_{i+1}$축을 지정하고 두 축이 서로 교차하지 않으면 두 축에 공통으로 수직인 법선을 지정하고, 공통 법선을 따라 $\hat X_i$축을 설정한다. 만약 두 축이 서로 교차하면 두 축이 만들어낸 평면에 수직한 방향으로 $\hat X_i$축을 설정한다. (이때 원점은 $\hat X_i$와 $\hat Z_i$에 의해 자동적으로 결정된다.)
- 오른손 법칙을 이용하여 $\hat Y_i$축을 설정한다.
- 마지막 링크 $n$의 좌표계는 관절 변수가 0일 때, 이웃하는 링크 $n-1$의 좌표계와 같은 방향을 가지도록 설정한다.
- 마지막으로 로봇의 영점 위치는 모든 관절 변수가 0인 위치로 지정한다. 회전 관절의 경우 이웃한 좌표계의 $x$축이 평행되고 같은 방향일 때, 직동 관절의 경우 링크 사이의 거리가 최소일 때를 영점 위치로 설정한다.
Manipulator Kinematics
$n$개의 링크로 구성되어 있는 Manipulator에 대해서 D-H 표기법에 따라 0번째 링크를 기준으로 링크 인자와 링크계를 설정한 이후에는, 연쇄적인 동차 변환(Homogeneous transformation)을 적용해서 Manipulator의 Base부에 대한 End-effector의 position과 orientation을 계산할 수 있다. 이를 정기구학(Forward kinematics) 또는 순기구학, 줄여서 기구학이라고 한다.
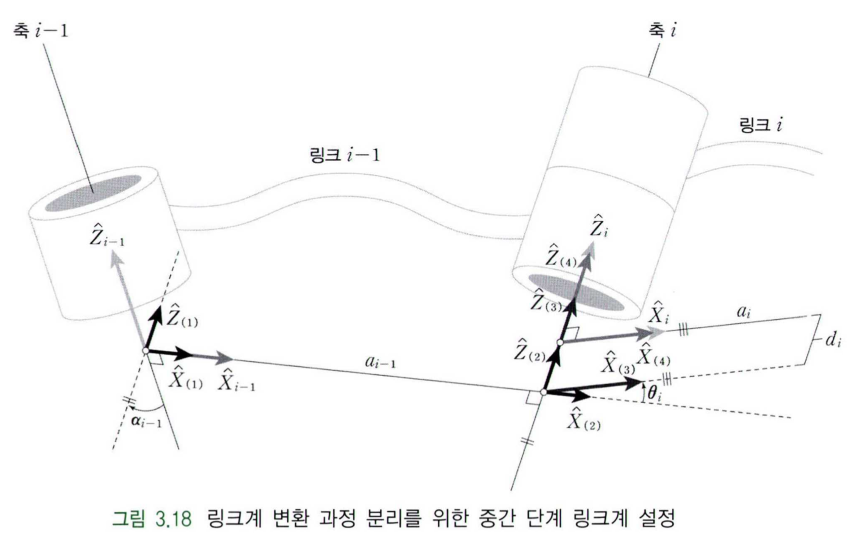
위 그림에서 링크계 {$i-1$}과 링크계 {$i$}를 구분하여 표현해놓았다. 링크계 {$i-1$}로부터 링크계 {$i$}로의 변환은 다음과 같은 순서로 분리해서 살펴볼 수 있다.
- 링크계 {$i-1$}이 $\hat X_{i-1}$축을 중심으로 각도 $\alpha_{i-1}$만큼 회전한다. $\rightarrow$ $\hat Z$축의 방향이 동일해진다.
- 링크계 {$i-1$}이 $\hat X_{i-1}$축을 따라서 거리 $a_{i-1}$만큼 이동한다. $\rightarrow$ $\hat Z$축이 동일해진다.
- 링크계 {$i-1$}이 $\hat Z_i$축을 중심으로 각도 $\theta_i$만큼 회전한다. $\rightarrow$ $\hat X$축의 방향이 동일해진다.
- 링크계 {$i-1$}이 $\hat Z_i$축을 따라서 거리 $d_i$만큼 이동한다. $\rightarrow$ $\hat X$축이 동일해진다.
1번을 제외한 단계에서의 링크계 {$i-1$}은 이전 모든 단계의 변환을 적용한 링크계를 의미한다.
위와 같은 순서로 링크계의 변환이 일어나면 링크계 {$i-1$}은 링크계 {$i$}와 일치하게 된다. 네 단계의 변환 과정은 각각 회전 또는 이동 후 만들어진 새로운 좌표계인 이동 좌표계가 기준 좌표계가 되어서 다음 변환이 일어나는 [상대 변환]임을 알 수 있다. 따라서, 각 단계의 변환 행렬을 앞에서부터 순차적으로 후위곱하여 연산하면 두 좌표계 사이의 변환을 나타내는 변환 행렬을 얻을 수 있다.
두 링크계 사이의 상대 관계를 나타내는 동차 변환 ${}^{i-1}T_i$는 [Position and Orientation - 2]의 변환 방정식을 이용해서 다음과 같이 정의할 수 있다.
\[{}^{i-1}T_i = Rot(\hat X_{i-1}, \alpha_{i-1}) ~Trans(\hat X_{i-1}, a_{i-1}) ~Rot(\hat Z_i, \theta_i) ~Trans(\hat Z_i, d_i)\]이때 $Rot(\hat X_{i-1}, \alpha_{i-1}) ~Trans(\hat X_{i-1}, a_{i-1})$는 동일한 축 $\hat X_{i-1}$에 의해 일어나는 변환이기에, $Rot$와 $Trans$의 순서를 바꾸어도 동일한 결과를 보여준다. $Rot(\hat Z_i, \theta_i) ~Trans(\hat Z_i, d_i)$의 경우도 마찬가지다.
이를 일반적인 행렬로 표현하면 다음과 같다.
\[\def\arraystretch{1.2} \begin{align*} {}^{i-1}T_{i} & = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha_{i-1} & -\sin\alpha_{i-1} & 0 \\ 0 & \sin\alpha_{i-1} & \cos\alpha_{i-1} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & a_{i-1} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos\theta_i & -\sin\theta_i & 0 & 0 \\ \sin\theta_i & \cos\theta_i & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} \cos\theta_i & -\sin\theta_i & 0 & a_{i-1} \\ \sin\theta_i\cos\alpha_{i-1} & \cos\theta_i\cos\alpha_{i-1} & -\sin\alpha_{i-1} & -\sin\alpha_{i-1}d_i \\ \sin\theta_i\sin\alpha_{i-1} & \cos\theta_i\sin\alpha_{i-1} & \cos\alpha_{i-1} & \cos\alpha_{i-1}d_i \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align*}\]일반적으로 Manipulator의 설계 시에 링크의 길이($a_i$)와 비틀림 각도($\alpha_i$)는 알려지기 때문에 고정값 또는 상수로 생각할 수 있다. 따라서, 두 링크간의 상대 운동량인 $\theta_i$와 $d_i$는 두 링크간의 상대 위치 및 방위를 결정하는 변수가 된다. 즉, 두 링크의 변환을 나타내는 ${}^{i-1}T_i$는 두 변수 $\theta_i$ 또는 $d_i$의 함수라고 볼 수 있다. 두 변수를 대표하는 새로운 변수를 $q_i(\theta_i, ~d_i)$라 하면 ${}^{i-1}T_i$는 다음과 같이 표현될 수 있다.
\[{}^{i-1}T_i = {}^{i-1}T_i(q_i)\]링크계 {$i$}에서 정의된 한 점에 대한 위치 벡터 ${}^iP$를 링크계 {$i-1$}에서의 상대적인 값으로 변환하기 위해서는 다음과 같이 표현할 수 있다.
\[{}^{i-1}P = {}^{i-1}T_i ~{}^iP\]또한 End-effector의 좌표계에 해당하는 링크계 {$n$}에서 정의된 한 점에 대한 위치 벡터 ${}^nP$는 다음과 같은 연산을 통해 링크계 {$0$}에서 표현될 수 있다.
\[\begin{align*} {}^0P &= {}^0T_1~{}^1T_2~\cdots~{}^{n-1}T_n~{}^nP \\ &={}^0T_n ~ {}^nP \end{align*}\]이때 ${}^0T_n$은 기준 좌표게 {0}에 기준한 좌표계 {n}의 pose, 즉 position(\(\mathbf{P}_{3\times1}\))과 orientation($\mathbf{R}_{3\times3}$)에 대한 정보를 담고 있다.
\[{}^0T_n = \begin{bmatrix} r_{11} & r_{12} & r_{13} & p_x \\ r_{21} & r_{22} & r_{33} & p_y \\ r_{31} & r_{32} & r_{33} & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{P}_{3\times1} \\ \mathbf{0}_{1\times3} & 1 \\ \end{bmatrix}\]관절 벡터와 관절 공간
$n$개의 링크로 연결되어 있는 Manipulator, 다시 말해 $n$ 자유도를 가지는 Manipulator의 모든 링크의 위치는 $n$개의 관절 변수의 조합으로 나타낼 수 있음을 살펴보았다. 이 독립된 관절 변수를 열벡터로 표현하면 $n \times 1$ 벡터가 된다. 이 $n$개의 변수들의 조합을 벡터 형태로 나타낸 것을 일반적으로 관절 벡터(Joint vector)라고 한다. 그리고, 이러한 관절 벡터에 의해서 형성되는 공간을 관절 공간(Joint space)이라고 한다.