Robotics - Chapter 6. Robot Statics
[5. Velocity Kinematics]에서는 속도와 관련된 로봇의 기구학적인 특성에 대해 살펴보았다. 일반적으로 강체로 구성되어 있는 로봇의 각 링크가 움직이기 위해서는 링크와 링크를 연결하고 있는 관절, 즉 조인트가 회전이나 병진 운동이 가능하도록 힘이 주어져야만 한다. 이번 포스팅에서는 관절의 회전 운동을 발생시킬 수 있는 힘(Force)과 회전에 필요한 돌림힘이라고도 불리는 토크(Torque) 또는 같은 의미로 사용되는 모멘트(Moment)에 대해서 논의한다.
모멘트
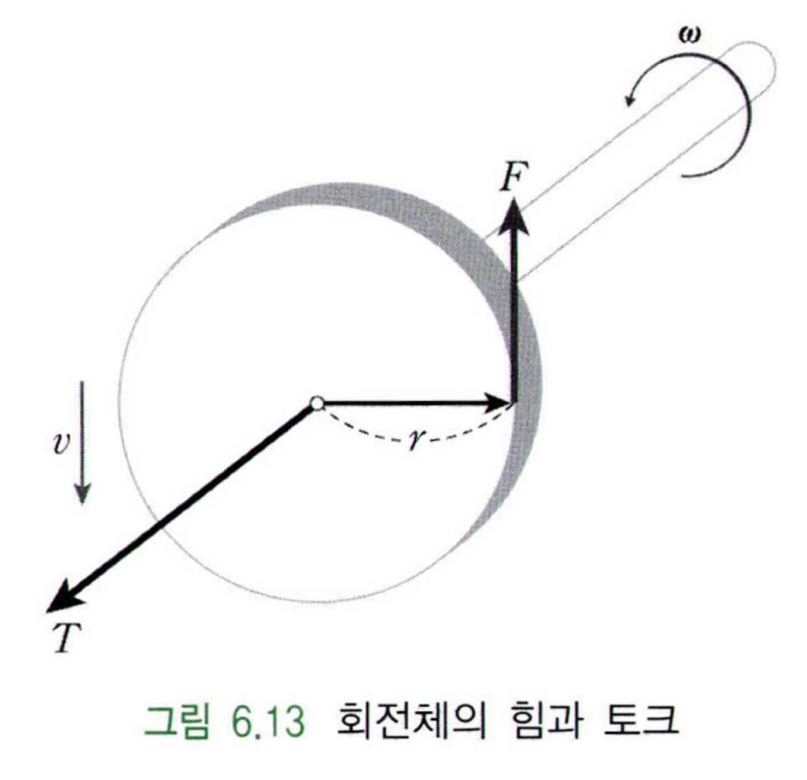
기구학적인 측면에서 모멘트는 회전력 또는 돌림힘(비틀림힘)으로 표현되는 토크와 비슷하다. 단, 토크는 실제로 회전이 이루어질 때의 회전하는 힘으로, 모멘트는 회전이 없을 때 회전하려는 힘 또는 실제 비틀림이 일어나서 회전을 막 시작하는 순간에 작용되는 힘을 의미한다. 그러나 서로 단위가 같고 본질적인 뜻이 같으므로 모멘트 또는 코트는 서로 호환되면서 사용된다. 엄밀하게는 물체를 회전시키려고 하는 힘의 작용을 모멘트 힘(Moment of force)라고 하지만, 간단하게 줄여서 모멘트라고 한다.
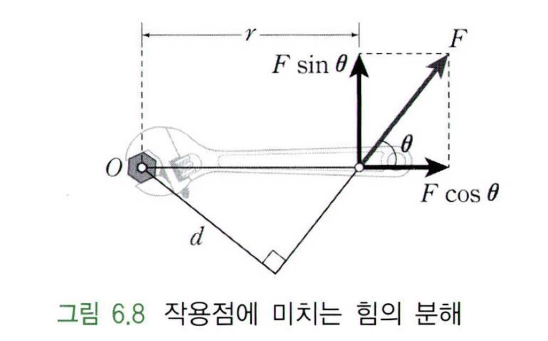
모멘트의 크기는 위 그림과 같이 작용된 힘과 힘이 작용한 위치로부터 회전축까지의 수직 거리를 곱한 값으로 다음과 같이 정의된다.
\[\begin{align*} M &= r \times F \\ &= r \times F\sin\theta \\ ||M||&= ||r||~||F||\sin\theta \end{align*}\]예상할 수 있듯이 힘의 방향이 수직일 때 최대 값을 가지며, 작용점과 동일한 선상에 작용되는 힘은 모멘트를 발생시키지 않는다. 그리고 같은 힘이라도 회전축과 힘의 작용점 사이의 거리(\(r\))에 따라 모멘트의 크기가 다르다는 점을 유의해야 한다.
모멘트에 의해 회전이 발생할 때, 모멘트의 축은 오른손 법칙을 따른다. 자세한 개념은 벡터곱을 참조하자.
일반적으로 물체는 현재의 상태를 계속 유지하려는 속성을 가지고 있고, 이러한 속성을 표현하는 물리량으로 관성(Inertia)이라는 개념을 사용한다. 예를 들어, 직선운동을 하는 어떤 물체에 힘을 가하면 그 물체는 힘과 가속도의 법칙(뉴턴의 제2법칙)에 따라 가속도 운동을 한다. 똑같은 힘을 가하더라도 물체의 가속도 즉, 운동의 변화 정도는 질량에 따라서 다르게 된다. 질량이 클수록 가속도는 작기 때문에 운동 변화가 크지 않지만, 질량이 작은 경우에는 같은 힘에 대해서도 가속도가 크기 때문에 운동의 변화도 커지게 된다. 반대로 질량이 큰 물체에 힘을 가해서 정지시키려면 음의 방향으로의 가속도가 작게 작용되기 때문에 정지하는데 오랜 시간이 필요하게 된다. 이때 ‘관성이 크다’라고 하는 것은 운동의 변화가 별로 없다는 의미로 사용되며, 일상적인 표현으로는 ‘묵직’하다는 느낌을 가지게 된다. 보통의 경우, 질량을 곧 관성의 크기로 생각하는 이유이기도 하다.
회전 운동에서도 이와 비슷한 개념을 사용하게 되는데, 똑같은 돌림힘을 가하더라도 물체에 따라서 각가속도가 달라진다. 만약 계속 회전을 유지하려는 성질이 크다면 각가속도는 작고, 회전을 유지하려는 성질이 작다면 각가속도가 크다고 할 수 있다. 이렇게 회전과 관련된 관성을 표현할 수 있는 물리량을 관성 모멘트(Moment of inertia) 또는 회전 관성(Rotational moment)이라고 한다. 관성과 마찬가지로 관성 모멘트가 클수록 각가속도의 변화는 작다.
스칼라 관성 모멘트를 일반적으로 관성 모멘트라고 하기도 하며, 보통의 회전 운동은 고정된 하나의 축에 대해서 회전과 관련된 각가속도, 각속도, 각운동량 등 모든 물리량이 완전하게 설명될 수 있기 때문에 스칼라 관성 모멘트를 사용한다.
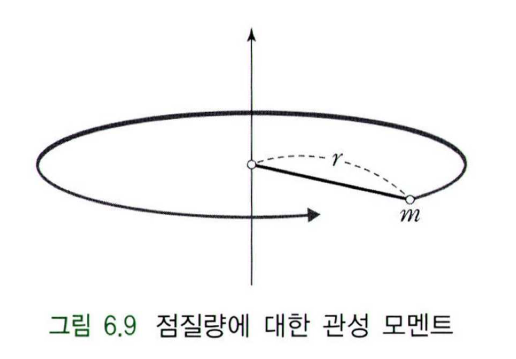
위와 같이 주어진 축을 중심으로 회전하는 점질량에 대한 관성 모멘트는 다음과 같이 정의된다.
\[I = mr^2\]여기서 $m$은 점질량, $r$은 회전축에서 점질량까지의 거리이다.
직선 운동에서의 힘 $F=ma$ 에서 질량 $m$이 관성 역할을 하는 것처럼, 회전 운동에서의 힘 $F=mr^2\alpha$ 에서 $mr^2$이 관성 모멘트($I$) 역할을 하게 된다.
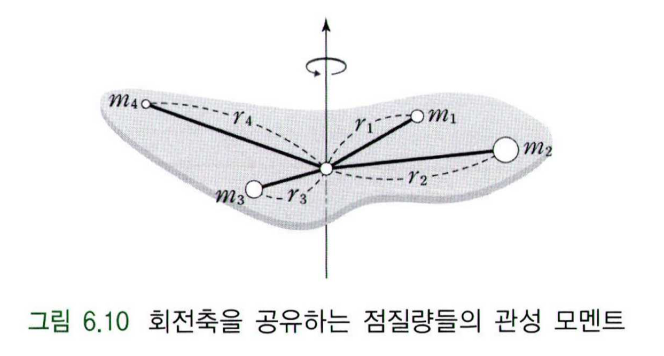
같은 축을 중심으로 회전하는 $n$개의 점질량을 다음과 같이 나타낼 수 있으며
이에 대한 총 관성 모멘트는 각 점질량들에 대한 관성 모멘트의 합이 되므로 다음과 같이 나타낼 수 있다.
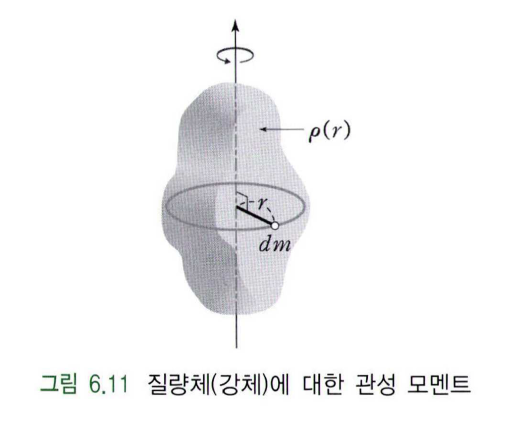
\[I = m_1r_1^2 + m_2r_2^2 + \cdots m_nr_n^2 = \sum_{i=1}^nm_ir_i^2\]점질량이 아닌 임의의 질량이 질량체(강체)에 연속적으로 분포하면, 다음 그림과 같이 나타낼 수 있다.
이때 미소 관성 모멘트 $dI$는 미소 질량 $dm$에 회전축으로부터 떨어진 거리를 곱한 것이 되므로
\[dI=r^2dm\]이다. 회전축으로부터 떨어진 거리 $r$에서의 미소 질량의 밀도가 $\rho(r)$이라면, 미소 질량 $dm$은 밀도와 미소 부피 $dV$의 곱으로 다음과 같이 표현할 수 있다.
\[dm = \rho(r)dV\]따라서 $dI$는 다음과 같고,
\[dI = \rho(r)r^2dV\]양변을 적분하면 강체의 관성 모멘트를 얻을 수 있다.
\[I = \int_m r^2~dm = \int_V \rho(r)r^2~dV\]관성 텐서
팽이나 자이로스코프와 같이 회전축이 변하는 복잡한 회전 운동은 회전축이 달라질 때마다 관성 모멘트가 바뀌게 되므로, 임의의 축에 대한 관성 모멘트를 구할 수 있는 관성 텐서(Inertia tensor)를 이용한다. 우선 관성 텐서를 유도하기 위해 필요한 각운동량(Angular momentum)부터 살펴보자.
각운동량
2차원 평면 상에 $n$개의 점질량이 있고, 질량 중심(Center of mass, $G$)을 기준으로 회전하는 상황을 가정해보자. 이때의 각운동량은 다음과 같다.
\[\begin{align*} H_G &= \sum_{i+1}^n(r^\prime_i \times m_i(\omega \times r^\prime_i)) = \sum_{i+1}^n m_i (r^{\prime}_i)^2 \omega \\ &= \int_m r' \times v'~dm \end{align*}\]마지막 줄은 점질량이 연속적으로 분포할 경우, 적분으로 나타낼 수 있음을 표현한 것이다.
위 식의 첫 줄은 각속도와 점질량의 위치 벡터는 서로 수직( $r’\cdot\omega=0$ )이므로 성립 가능한 식이다. 만약 3차원이라면 두 벡터가 수직임을 보장할 수 없으므로 다음과 같이 식이 전개된다.
\[H_G = \int_m r' \times (\omega \times r')~dm = \int_m[(r'\cdot r')\omega - (r'\cdot\omega)r']~dm\]직교 좌표계에서 $r’ = x’i + y’j + z’k$ 이고 $\omega = \omega_xi + \omega_yj + \omega_zk$ 이라 하자. 모든 위치 벡터 $r’$은 질량 중심을 기준으로 정의되었고, 회전축 $\omega$는 질량 중심을 지나가도록 설정되었다. 이때 다음과 같은 식을 만족한다.
\[\begin{align*} H_G &= \bigg( \omega_x\int_m(x'^2+y'^2+z'^2)~dm - \int_m(\omega_xx'+\omega_yy'+\omega_zz')x'~dm \bigg)i \\ &+ \bigg( \omega_y\int_m(x'^2+y'^2+z'^2)~dm - \int_m(\omega_xx'+\omega_yy'+\omega_zz')y'~dm \bigg)j \\ &+ \bigg( \omega_z\int_m(x'^2+y'^2+z'^2)~dm - \int_m(\omega_xx'+\omega_yy'+\omega_zz')z'~dm \bigg)k \\ \\ &= (~~I_{xx}\omega_x - I_{xy}\omega_y - I_{xx}\omega_z)i \\ &+ (-I_{yx}\omega_x + I_{yy}\omega_y - I_{yz}\omega_z)j \\ &+ (-I_{zx}\omega_x - I_{zy}\omega_y + I_{zz}\omega_z)k \\ \end{align*}\]이때 $I$와 관련된 식은 다음과 같다.
\[I_{xx} = \int_m(y'^2 + z'^2)~dm~~, ~~~~~ I_{yy} = \int_m(x'^2 + z'^2)~dm~~, ~~~~~ I_{zz} = \int_m(x'^2 + y'^2)~dm\] \[I_{xy}=I_{yx}=\int_mx'y'~dm~~, ~~~~~ I_{xz}=I_{zx}=\int_mx'z'~dm~~, ~~~~~ I_{yz}=I_{zy}=\int_my'z'~dm\]그리고 $H_G$를 다음과 같이 행렬 형태로 나타낼 수 있다.
\[\begin{pmatrix} ~H_{Gx}~ \\ ~H_{Gy}~ \\ ~H_{Gz}~ \end{pmatrix} = \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{yx} & I_{yy} & -I_{yz} \\ -I_{zx} & -I_{zy} & I_{zz} \end{pmatrix} \begin{pmatrix} ~\omega_{x}~ \\ ~\omega_{y}~ \\ ~\omega_{z}~ \end{pmatrix}\] \[H_G = [I_G]\omega\]이때 $[I_G]$가 관성 텐서이다.
관성 텐서
만약 원점이 질량 중심이 아니라, 회전축 상의 다른 점 $O$라면 어떻게 될까? 원점 $O$를 기준으로 한 위치 벡터 $r = xi + yj + zk$ 이고, $r_G = x_Gi + y_Gj + z_Gk$ 라 할 때 $r = r_G + r’$ 이라 하자. 이때 다음과 같은 식을 만족한다. 우선 아래 첨자의 종류가 동일한 $I$부터 살펴보자.
\[\begin{align*} (I_{xx})_O &= \int_m(y^2+z^2)~dm \\ &= \int_m\bigg((y_G+y')^2+(z_G+z')^2\bigg)~dm \\ &= \int_m(y'^2 + z'^2)~dm + 2\bigg(y_G\int_my'~dm + z_G\int_mz'~dm\bigg) + (y_G^2 + z_G^2)\int_m~dm \\ &= \int_m(y'^2 + z'^2)~dm + m(y_G^2 + z_G^2) \\ &= I_{xx} + m(y_G^2 + z_G^2) \end{align*}\]이와 비슷하게 다음도 성립한다.
\[(I_{yy})_O = I_{yy}+ m(x_G^2 + z_G^2), ~~~~~ (I_{zz})_O = I_{zz}+ m(x_G^2 + y_G^2)\]이번에는 아래 첨자의 종류가 다른 $I$를 살펴보자.
\[\begin{align*} (I_{xy})_O &= \int_m xy~dm \\ &= \int_m(x_G+x')(y_G+y')~dm \\ &= \int_mx'y'~dm + x_G\int_my'~dm + y_G\int_mx'~dm + x_Gy_G\int_m~dm \\ &= \int_mx'y'~dm + mx_Gy_G \\ &= I_{xy} + mx_Gy_G \end{align*}\]마찬가지로 비슷하게 다음도 성립한다.
\[(I_{xz})_O=(I_{zx})_O=I_{xz} + mx_Gz_G~~, ~~~~~ (I_{yz})_O=(I_{zy})_O=I_{yz} + my_Gz_G\]위 식들은 모두 질량 중심의 성질( $\int_m x’~dm =\int_m y’~dm =\int_m z’~dm =0$ )에 따라 유도되었다.
그러므로 $[I_O]$와 $[I_G]$ 사이에는 다음과 같은 관계가 성립한다.
\[I_O = I_G + m[(r_G\cdot r_G)E - r_G\otimes r_G]\]이때 $E$는 단위행렬이고, $r_G\otimes r_G = r_G^{}r_G^T$ 를 의미한다.
만약 임의의 $xyz$ 축에 대해 관성 텐서 $[I]$를 구해놓았는데, 회전 행렬 $[R]$에 의해 회전된 좌표계에서의 관성 텐서 $[I’]$을 구하고 싶다면 다음과 같이 쉽게 구할 수 있다.
\[\begin{align*} H' &= [R]H \\ &= [R][I]\omega \\ &= [R][I][R^T][R]\omega \\ &= \Big([R][I][R^T]\Big)\Big([R]\omega\Big) \\ &= [I']\Big([R]\omega\Big) \\ \end{align*}\]위 식은 임의의 원점과 좌표계에서 정의된 모든 관성 텐서 $[I]$에 대해 성립한다.
토크
병진 운동에서 힘, 위치, 속도, 가속도, 질량 등의 물리량이 있는 것처럼, 회전 운동에서는 토크, 각도, 각속도, 각가속도, 관성 모멘트 등의 물리량이 존재한다.
토크(Torque)는 힘과 다음과 같은 관계를 갖는다.
\[T = r \times F\]앞서 모멘트와 토크가 같은 개념으로 소개되었던 것처럼, 식도 동일한 형식을 가진다.
위 식을 회전 관성을 이용하여 다시 나타내면 다음과 같다.
\[T = I\alpha\]이때 $I$는 관성 모멘트, $\alpha$는 각가속도이다.
모멘트는 일반적으로 고정된 기준점에 대해 일정한 거리만큼 떨어져 있는 지점에서 측정된 물리량이다. 이와 달리 토크는 물체에 작용하여 물체를 회전시키는 원인이 되는 물리량을 의미한다. 다시 말해 회전력이 직접 회전 중심에 작용하는 경우에 토크라는 용어를 사용하게 된다. 두 물리량이 같은 식과 값을 가지기는 하지만, 실제로 힘의 작용이 어디서 일어나는가에 따라 종류가 나누어지게 된다.
Manipulator 정역학
로봇을 이용해서 용접을 하거나 드릴을 이용해서 타공 등의 작업을 하는 경우, 로봇의 End-effector에는 작업의 모든 과정에서 일정한 힘의 작용을 필요로 한다. 용접 시에는 철판과 용접봉과의 정적 평형이 이루어져야 철판의 찌그러짐이나 다른 변형이 발생하지 않고 올바른 용접을 할 수 있으며, 드릴 작업시에는 타공 방향으로의 지속적인 힘이 가해져야만 볼트나 나사를 결합하는 데 필요한 구멍을 뚫을 수 있다.
외력 또는 힘을 받는 물체는 일반적으로 정지 또는 운동 상태로 해석할 수 있는데, 이러한 분야를 다루는 학문을 역학이라 한다. 로봇공학에서는 전통적인 고전 역학 즉, 뉴턴의 운동 법칙에 기초하는 뉴턴 역학을 기반으로 힘의 작용에 의한 로봇의 상태를 설명한다. 특히 힘을 받는 로봇이나 End-effector로 용접 작업을 할 때와 같이 특정한 순간에 정지 상태인 경우, 정역학(Statics)의 기법을 통해서 힘의 정적 상태 또는 정적 평형(Static equilibrium) 상태의 관점에서 로봇과 힘의 관계를 해석한다. 로봇의 운동 상태가 지속적으로 변화되는 드릴 작업과 같은 경우, 로봇의 운동을 동역학(Dynamics) 기법을 통해서 로봇과 힘의 관계를 설명하게 된다.
Manipulator 정역학은 Manipulator의 말단에 가해지는 힘(힘과 모멘트)과 관절에 가해진 힘(직동 관절의 경우는 힘, 회전 관절의 경우는 토크)과의 관계를 구하는 것을 목적으로 한다. 예를 들어, 말단의 끝에 접촉하는 물체를 밀거나 들고 있는 물체를 지지하는데 필요한 적합한 힘 또는 평형(균형) 상태를 이루기 위한 관절 조건을 풀어내기 위함이라고 할 수 있다.
Manipulator는 베이스부로부터 End-effector까지 연속적으로 연결된 링크와 관절로 구성되어 있기 때문에, 힘과 모멘트가 한 링크에서 다음 링크로 어떤 영향력을 주게 되어 마지막에 연결되어 있는 말단 장치에 어떠한 힘과 모멘트가 전달되는지를 계산할 필요가 있다. 이러한 힘과 모멘트의 전달을 ‘전파(Propagation)’라고 한다.
Manipulator의 End-effector의 정역 해석을 위한 단계는 다음과 같다.
- 고전 역학에서 다수의 링크 구조를 가지는 구조물을 하나의 구조물 형태로 풀어서 해석하는 것처럼 Manipulator의 모든 관절을 고정시킴으로써 개념적으로 단일 구조물 또는 단일 링크로 이루어진 것과 같은 상태가 되도록 한다.
- 각 링크에 링크계를 부여한 후, 링크계에 따라 힘의 분해 및 합력 관계를 표현한다.
- Manipulator가 정적 평형 상태를 유지할 수 있도록 관절축에 작용되는 정토크를 계산한다.
- End-effector에 작용하는 외력 또는 정하중을 지지할 수 있는 반력 즉, 관절 토크 조합을 계산한다.
정적 평형(Static equilibrium): 입자의 알짜힘이 0인 상태, 즉 어떤 계의 모든성분에 대한 힘과 돌림힘 각각의 합이 0이 되는 상태를 의미한다. 또한 움직임(Motion)이 존재하지 않아야 한다.
정토크(Static torque): 정적 평형 상태에서의 토크를 의미한다.
정하중(Static load): 동력이 공급되지 않고 움직이지 않는 상태에 있을 때 가해지는 하중을 의미한다.
정적 평형과 동적 평형(Dynamic equilibrium) 모두 모든 힘/토크의 합이 0이 된다. 즉, 두 상태 모두 Manipulator의 관절 변수의 시간에 대해 두 번 미분한 값(가속도)이 0이 된다( $\ddot q = 0$ ). 하지만 정적 평형의 경우는 대상의 움직임(Motion)이 없고, 동적 평형은 움직임이 있는 상태이다. 다시 말해 정적 평형의 경우 관절 변수의 속도 $\dot q = 0$ 이고, 동적 평형의 경우 관절 변수의 속도($\dot q$)가 0이 아닌 값을 가질 수 있다.
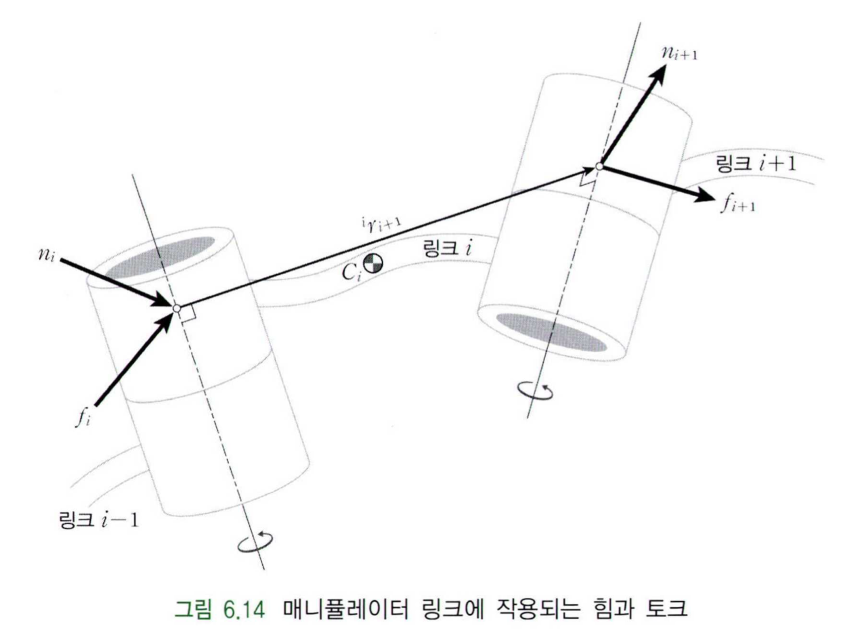
위 그림은 인접하는 두 링크의 힘과 모멘트의 작용을 나타내고 있다. $f_i$와 $n_i$는 $i-1$번째 링크가 $i$번째 링크에 작용하는 힘과 모멘트 벡터를 나타내고, $C_i$ 는 질량 중심을 의미하고, ${}^ir_{i+1}$은 링크계 설정 방법에 의해서 정의된 링크 $i$의 길이를 의미한다. Manipulator가 $i+1$ 개의 링크로 구성되어 있다면, 외부 환경과 직접적인 상호작용이 일어나는 부분은 $i+1$번째 관절에 연결된 링크의 말단 또는 End-effector라고 할 수 있다.
우선 링크의 질량 중심에서 중력 방향으로 발생하는 중력 효과는 무시한다고 하자. 링크 $i+1$ 의 말단 부분에서 외부 환경에 힘 $F$를 작용하고 있다면, 링크 $i+1$ 기준으로 해당 지점에서 반력 $-F$가 작용하게 된다. 링크 $i+1$ 내부 힘의 합력은 힘의 평형 특성( $\sum F=0$ )에 의해 0이 되어야 하므로, 관절 $i+1$에 작용하는 힘은 $f_{i+1}=F$ 가 된다. 링크 $i$ 의 끝부분은 관절 $i+1$과 연결되어 있으므로 반작용으로 인해 $-f_{i+1}$의 힘을 받는다. 마찬가지로 힘의 평형 특성으로 관절 $i$에 작용하는 힘은 $f_i=f_{i+1}=F$ 가 된다. 즉, $f_1 = f_2 = \cdots = f_{i+1}$ 을 만족하게 되고, 따라서 다음과 같은 식이 성립한다.
\[{}^if_i = {}^if_{i+1}\]그리고 링크계 {$i$}의 원점에서의 모멘트도 힘의 평형 특성으로 인해 다음과 같이 표현할 수 있다.
\[\begin{align*} {}^in_i &= {}^in_{i+1} + {}^ir_{i+1} \times {}^if_{i+1} \\ &= {}^iR_{i+1}{}^{i+1}n_{i+1} + {}^ir_{i+1} \times {}^if_{i} \end{align*}\]이렇게 하면 Manipulator의 베이스부로부터 End-effector까지 순차적으로 외부 환경과 정적 평형 상태를 이루기 위한 모든 관절의 구동부에서 작용되는 힘과 모멘트를 구할 수 있게 된다.
위 그림을 참고하면 링크와 관련된 힘과 토크를 조금 더 쉽게 이해할 수 있다.
Manipulator는 공간상에 존재하기 때문에, 위 식에서 벡터 $f_i$와 $n_i$는 3차원 벡터가 된다. 하지만 Manipulator의 관절은 [3. Manipulator Kinematics]에서 살펴보았듯이 $z$축을 기준으로 회전/직선 운동을 하기 때문에 $z$축 방향으로만 유효한 힘이나 모멘트가 존재하게 된다. 즉, 힘과 모멘트 벡터는 관절축에 해당하는 요소를 제외하면 기구 자체의 구조에 의해서 상쇄된다. 따라서 Manipulator의 정적 평형 상태를 유지하기 위한 관절 토크는 관절축 벡터와 링크에 작용하는 모멘트 벡터의 내적으로 구할 수 있다.
\[\tau_i = {}^in_i^T {}^iz_i^{}\]위 식은 회전 관절일 경우에 성립하는 식이고, 직동형 관절에서는 다음 식을 만족하게 된다.
\[F_i = {}^if_i^T {}^iz_i^{}\]따라서 Manipulator의 End-effector의 힘과 토크로 각 링크의 힘과 토크를 독립적으로 나타낼 수 있음이 자명하다.
힘과 모멘트와 자코비안
어떤 물체에 힘이 작용해서 움직이는 경우 즉, 변위의 차이가 발생하는 경우에는 일(Work) 또는 에너지의 관점에서 운동에 대한 해석이 가능해진다. 일은 힘이 작용함에 따라 일정한 거리를 움직인 것으로, 에너지의 단위인 줄($J$)이 사용되며, $1J$은 물체에 $1N$의 힘이 작용하는 동안 물체가 $1m$ 이동했을 때 힘이 한 일을 의미한다.
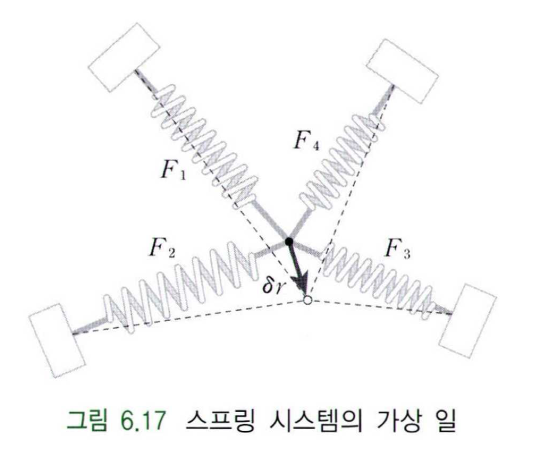
앞서 언급한 것처럼 정적 평형은 물체에 가해지는 전체 힘의 합과 전체 토크의 합이 0이 되는 상태이다. 실제로 정적 평형을 계산하기 위해서는 외부에 가해진 힘뿐만 아니라 반력과 내력, 각 관절의 모든 힘과 조건을 고려해야 하기 때문에 복잡도가 매우 높아지게 된다. 하지만 가상 일의 원리(Principle of virtual work)를 적용하면, 가상 변위와 관련된 힘만을 고려하면 되기 때문에 반력이나 내력 등의 영향을 제거할 수 있고, 구속 조건의 적용과 정역 해석이 간단해진다.
어떤 시스템의 가상 변위(Virtual displacement, $\delta r$)에 대해서 시스템이 한 일을 가상 일(Virtual work, $\delta W$)이라 한다. 그리고, 가상 일의 원리는 시스템이 평형 상태에 있을 때, 가상 변위에 대한 가상 일이 0이 되도록 하는 것이다. 즉, 정적 평형 상태에서 시스템에 가해지는 모든 힘의 합이 0이 되는 것과 동일하다고 할 수 있다.
위와 같은 정적 평형 상태를 고려하면, 가상 변위에 대한 가상 일은 다음과 같이 나타낼 수 있다.
\[\delta W = \sum F_i \cdot \delta r = 0 ~~~\to~~~ \sum F_i = 0\]직교 좌표 공간에서 Manipulator의 End-effector에 작용한 힘 $F$에 의해 발생한 변위 $\delta X$에 대한 가상 일은
\[\delta W = F \cdot \delta X\]와 같이 정의할 수 있다.
End-effector에 가해진 힘 $F$에 의해 발생한 $\delta X$만큼의 변화는 정적 평형 상태를 유지하기 위해서 구동부 즉, Manipulator를 구성하는 관절부의 반력을 유발하는 요인이 되고, 작용-반작용의 원리에 의해 End-effector에서 발생한 일과 동일한 값을 가져야만 한다. 따라서, 관절부에 작용하는 힘은 관절 토크($\tau$)로, 변위는 각변위($\theta=q$)로 대응시킬 수 있으므로 다음 식이 성립한다.
\[F \cdot \delta X = \tau \cdot \delta q\]위 식을 $n$ 자유도 Manipulator로 확장하면, 힘 $F$는 End-effector에 작용하는 직교 좌표계 상의 $n\times1$ 힘 벡터이며, $\delta X$는 End-effector의 $n\times1$ 변위 벡터이다. 또한 $\tau$는 관절 공간에서의 $n\times1$ 토크 벡터이며, $\delta q$는 관절 공간에서 $n\times1$ 관절 변위 벡터이다. 따라서 다음과 같이 표현할 수 있다.
\[F^T\delta X = \tau^T \delta q\]직교 좌표 공간에서 Manipulator의 End-effector의 속도를 관절의 속도로 전환할 수 있는 [자코비안의 정의]를 사용하면 변위에 대한 각변위의 대응 관계를 다음과 같이 나타낼 수 있고, 이를 위 식에 대입하여 정리할 수 있다.
\[\delta X = J \delta q\] \[\begin{align*} F^TJ \delta q &= \tau^T \delta q \\ F^TJ &= \tau^T \\ J^TF &= \tau \end{align*}\]위 식의 자코비안은 시사하는 바가 매우 크다. End-effector에 작용하는 힘과 평형을 이룰 수 있는 관절 토크를 자코비안만으로도 간단하게 구할 수 있기 때문이다. 즉, 직관적으로 조작하고 제어 가능한 관절 공간의 정보를 통해서 Manipulator의 힘 제어를 할 수 있음을 보여주고 있다.
그러나 [속도 관계]에서도 언급되었던 것처럼 힘과 토크 관계에서도 자코비안의 특이점이 존재하기 때문에, 이 특이점에서는 관절 토크의 어떠한 조합으로도 말단 장치에 적합한 힘을 작용시킬 수 없는 영역이 있다는 것을 명심할 필요가 있다.
직교 좌표 공간에서의 속도와 힘의 변환
Manipulator는 작업 목적에 따라 End-effector에 용접봉이나 그리퍼 등의 공구를 부착해서 사용하는 것이 일반적이다. 공구와 외부 환경이 직접적으로 상호작용하는 부분에 다양한 센서를 부착하여, 힘이나 속도 등의 정보를 통해 적절히 제어할 수도 있지만, 경우에 따라서는 센서 부착이 어려울 때가 있다. 이러한 경우, 관절의 다른 부분에 센서를 부착하여 관절 좌표계의 속도와 힘 관계를 말단 좌표계 또는 공구 좌표계로 변환함으로써 말단 또는 공구의 속도와 힘을 계산할 수 있다.
$6 \times 1$ 벡터로 구성되는 일반적인 Manipulator의 속도 벡터와 힘 벡터를 다음과 같이 나타낼 수 있다.
\[\nu = \begin{bmatrix} v \\ \omega \end{bmatrix}_{6\times1} ~~,~~~~~ \Im = \begin{bmatrix} F \\ N \end{bmatrix}_{6\times1}\]속도의 변환 행렬
5장의 [Manipulator의 링크 운동 해석]에서 살펴보았던 것처럼, 링크계 간의 속도/각속도의 관계식을 이용하면 한 링크계의 속도/각속도를 다른 링크계에서 나타낼 수 있었다. 일반화 되어 있는 한 링크계 {$B$}의 속도/각속도를 링크계 {$A$}에서 나타내면 다음과 같다.
\[\begin{align*} &~~~~~{}^{A}v_{A} = {}^{A}R_B({}^Bv_B + {}^B\omega_B\times{}^BP_{Aorg}) + \dot d_{A}{}^{A}\hat Z_{A} ~~~~~~~~,~~~~~ {}^{A}\omega_{A} = {}^{A}R_B{}^B\omega_B + \dot\theta_{A}{}^{A}\hat Z_{A} \end{align*}\]그런데 정적 평형 상태에서 관절 변수의 시간 미분 값 즉, 속도 $\dot q=0$ 이므로 다음과 같이 식을 정리할 수 있고,
\[\begin{align*} {}^{A}v_{A} &= {}^{A}R_B({}^Bv_B + {}^B\omega_B\times{}^BP_{Aorg}) ~~~~~~~~~~~~~~~~~~~~~~~~~,~~~~~ {}^{A}\omega_{A} = {}^{A}R_B{}^B\omega_B~~~~~~~~~~~ \\ &= {}^{A}R_B {}^Bv_B + ({}^{A}R_B {}^B\omega_B) \times ({}^{A}R_B {}^BP_{Aorg}) \\ &= {}^{A}R_B {}^Bv_B + ({}^{A}R_B {}^B\omega_B) \times (-{}^AP_{Borg}) \\ &= {}^{A}R_B {}^Bv_B + ({}^AP_{Borg}) \times ({}^{A}R_B {}^B\omega_B) \\ &= {}^{A}R_B {}^Bv_B + [{}^AP_{Borg}]_\times {}^{A}R_B {}^B\omega_B \\ \\ \end{align*}\]이를 행렬로 표현할 수 있다.
\[\def\arraystretch{1.2} \begin{align*} \begin{bmatrix} {}^{A}v_{A} \\ {}^{A}\omega_{A} \end{bmatrix} &= \begin{bmatrix} {}^AR_B & [{}^AP_{Borg}]_\times {}^AR_B \\ 0 & {}^AR_B \end{bmatrix} \begin{bmatrix} {}^{B}v_{B} \\ {}^{B}\omega_{B} \end{bmatrix} \\ \\ {}^A\nu_A &= {}^A(T_\nu)_B~{}^B\nu_B \end{align*}\]힘의 변환 행렬
앞서 구한 힘에 관한 식은 다음과 같다.
\[\begin{align*} {}^if_i = {}^if_{i+1} ~~~~~~~~~~~~~~, ~~~~~~~~~~~~~~ {}^in_i &= {}^in_{i+1} + {}^ir_{i+1} \times {}^if_{i+1} \\ &= {}^iR_{i+1}{}^{i+1}n_{i+1} + {}^ir_{i+1} \times {}^if_{i} \end{align*}\]이 또한 링크계 {$B$}와 링크계 {$A$} 사이의 관계식으로 나타내면 다음과 같다.
\[\begin{align*} ~~~~~~~~~~~{}^Af_A = {}^AR_{B}{}^Bf_{B} ~~~~~~,~~~~~~~~~~~~~ {}^An_A &= {}^An_{B} + {}^AP_{Borg} \times {}^Af_{B} \\ &= {}^AR_{B}{}^{B}n_{B} + {}^AP_{Borg} \times {}^AR_{B} {}^Bf_{B} \end{align*}\]그리고 이를 행렬로 표현하면 다음과 같다.
\[\def\arraystretch{1.2} \begin{align*} \begin{bmatrix} {}^{A}F_{A} \\ {}^{A}N_{A} \end{bmatrix} &= \begin{bmatrix} {}^AR_B & 0 \\ [{}^AP_{Borg}]_\times {}^AR_B & {}^AR_B \end{bmatrix} \begin{bmatrix} {}^{B}F_{B} \\ {}^{B}N_{B} \end{bmatrix} \\ \\ {}^A\Im_A &= {}^A(T_\Im)_B~{}^B\Im_B \end{align*}\]이때 속도에서의 변환 행렬과 힘에서의 변환 행렬은 서로 전치 관계에 있는 것을 확인할 수 있다. 그러므로 다음과 같이 힘에서의 변환 행렬을 속도에서의 변환 행렬로부터 구할 수 있다. \({}^A(T_\Im)_B^{} = {}^A(T_\nu)_B^T\)